Probability

How likely something is to happen.

Many events can't be predicted with total certainty. The best we can say is how likely they are to happen, using the idea of probability.

Tossing a Coin  When a coin is tossed, there are two possible outcomes: heads (H) or tails (T) We say that the probability of the coin landing H is ½. And the probability of the coin landing T is ½.

Throwing Dice  When a single die is thrown, there are six possible outcomes: 1, 2, 3, 4, 5, 6. The probability of any one of them is 1/6.

Probability 

In general:

Probability of an event happening =		Number of ways it can happen
		Total number of outcomes

Example: the chances of rolling a "4" with a die

Number of ways it can happen: 1 (there is only 1 face with a "4" on it)

Total number of outcomes: 6 (there are 6 faces altogether)

So the probability =	1
	6

Example: there are 5 marbles in a bag: 4 are blue, and 1 is red. What is the probability that a blue marble will be picked?

Number of ways it can happen: 4 (there are 4 blues)

Total number of outcomes: 5 (there are 5 marbles in total)

So the probability =	4	= 0.8
	5

Probability Line

You can show probability on a Probability Line:

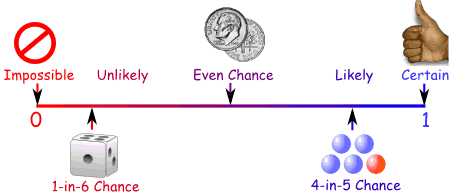
Probability is always between 0 and 1

Probability is Just a Guide

Probability does not tell us exactly what will happen, it is just a guide

Example: toss a coin 100 times, how many Heads will come up?

Probability says that heads have a ½ chance, so we would expect 50 Heads.

But when you actually try it out you might get 48 heads, or 55 heads ... or anything really, but in most cases it will be a number near 50.

Learn more at Probability Index.

Words

Some words have special meaning in Probability:

Experiment: an action where the result is uncertain.

Tossing a coin, throwing dice, seeing what pizza people choose are all examples of experiments.

Sample Space: all the possible outcomes of an experiment

Example: choosing a card from a deck

There are 52 cards in a deck (not including Jokers)

So the Sample Space is all 52 possible cards: {Ace of Hearts, 2 of Hearts, etc... }

The Sample Space is made up of Sample Points:

Sample Point: just one of the possible outcomes

Example: Deck of Cards

• the 5 of Clubs is a sample point
• the King of Hearts is a sample point

"King" is not a sample point. As there are 4 Kings that is 4 different sample points.

Event: a single result of an experiment

Example Events:

• Getting a Tail when tossing a coin is an event
• Rolling a "5" is an event.

An event can include one or more possible outcomes:

• Choosing a "King" from a deck of cards (any of the 4 Kings) is an event
• Rolling an "even number" (2, 4 or 6) is also an event

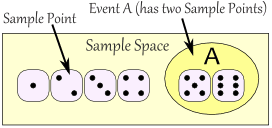The Sample Space is all possible outcomes. A Sample Point is just one possible outcome. And an Event can be one or more of the possible outcomes.

Probability of a Single Event

If you roll a six-sided die, there are six possible outcomes, and each of these outcomes is equally likely. A six is as likely to come up as a three, and likewise for the other four sides of the die. What, then, is the probability that a one will come up? Since there are six possible outcomes, the probability is 1/6. What is the probability that either a one or a six will come up? The two outcomes about which we are concerned (a one or a six coming up) are called favorable outcomes. Given that all outcomes are equally likely, we can compute the probability of a one or a six using the formula:



In this case there are two favorable outcomes and six possible outcomes. So the probability of throwing either a one or six is 1/3. Don't be misled by our use of the term "favorable," by the way. You should understand it in the sense of "favorable to the event in question happening." That event might not be favorable to your well-being. You might be betting on a three, for example.

The above formula applies to many games of chance. For example, what is the probability that a card drawn at random from a deck of playing cards will be an ace? Since the deck has four aces, there are four favorable outcomes; since the deck has 52 cards, there are 52 possible outcomes. The probability is therefore 4/52 = 1/13. What about the probability that the card will be a club? Since there are 13 clubs, the probability is 13/52 = 1/4.

Let's say you have a bag with 20 cherries: 14 sweet and 6 sour. If you pick a cherry at random, what is the probability that it will be sweet? There are 20 possible cherries that could be picked, so the number of possible outcomes is 20. Of these 20 possible outcomes, 14 are favorable (sweet), so the probability that the cherry will be sweet is 14/20 = 7/10. There is one potential complication to this example, however. It must be assumed that the probability of picking any of the cherries is the same as the probability of picking any other. This wouldn't be true if (let us imagine) the sweet cherries are smaller than the sour ones. (The sour cherries would come to hand more readily when you sampled from the bag.) Let us keep in mind, therefore, that when we assess probabilities in terms of the ratio of favorable to all potential cases, we rely heavily on the assumption of equal probability for all outcomes.

Here is a more complex example. You throw 2 dice. What is the probability that the sum of the two dice will be 6? To solve this problem, list all the possible outcomes. There are 36 of them since each die can come up one of six ways. The 36 possibilities are shown below.

Die 1	Die 2	Total		Die 1	Die 2	Total		Die 1	Die 2	Total
1	1	2		3	1	4		5	1	6
1	2	3		3	2	5		5	2	7
1	3	4		3	3	6		5	3	8
1	4	5		3	4	7		5	4	9
1	5	6		3	5	8		5	5	10
1	6	7		3	6	9		5	6	11
2	1	3		4	1	5		6	1	7
2	2	4		4	2	6		6	2	8
2	3	5		4	3	7		6	3	9
2	4	6		4	4	8		6	4	10
2	5	7		4	5	9		6	5	11
2	6	8		4	6	10		6	6	12

You can see that 5 of the 36 possibilities total 6. Therefore, the probability is 5/36.

If you know the probability of an event occurring, it is easy to compute the probability that the event does not occur. If P(A) is the probability of Event A, then 1 - P(A) is the probability that the event does not occur. For the last example, the probability that the total is 6 is 5/36. Therefore, the probability that the total is not 6 is 1 - 5/36 = 31/36.

Probability of Two (or more) Independent Events

Events A and B are independent events if the probability of Event B occurring is the same whether or not Event A occurs. Let's take a simple example. A fair coin is tossed two times. The probability that a head comes up on the second toss is 1/2 regardless of whether or not a head came up on the first toss. The two events are (1) first toss is a head and (2) second toss is a head. So these events are independent. Consider the two events (1) "It will rain tomorrow in Houston" and (2) "It will rain tomorrow in Galveston" (a city near Houston). These events are not independent because it is more likely that it will rain in Galveston on days it rains in Houston than on days it does not.

Probability of A and B

When two events are independent, the probability of both occurring is the product of the probabilities of the individual events. More formally, if events A and B are independent, then the probability of both A and B occurring is:

P(A and B) = P(A) x P(B)

where P(A and B) is the probability of events A and B both occurring, P(A) is the probability of event A occurring, and P(B) is the probability of event B occurring.

If you flip a coin twice, what is the probability that it will come up heads both times? Event A is that the coin comes up heads on the first flip and Event B is that the coin comes up heads on the second flip. Since both P(A) and P(B) equal 1/2, the probability that both events occur is

1/2 x 1/2 = 1/4

Let's take another example. If you flip a coin and roll a six-sided die, what is the probability that the coin comes up heads and the die comes up 1? Since the two events are independent, the probability is simply the probability of a head (which is 1/2) times the probability of the die coming up 1 (which is 1/6). Therefore, the probability of both events occurring is 1/2 x 1/6 = 1/12.

One final example: You draw a card from a deck of cards, put it back, and then draw another card. What is the probability that the first card is a heart and the second card is black? Since there are 52 cards in a deck and 13 of them are hearts, the probability that the first card is a heart is 13/52 = 1/4. Since there are 26 black cards in the deck, the probability that the second card is black is 26/52 = 1/2. The probability of both events occurring is therefore 1/4 x 1/2 = 1/8.

See the section on conditional probabilities on this page to see how to compute P(A and B) when A and B are not independent.

Probability of A or B

If Events A and B are independent, the probability that either Event A or Event B occurs is:

P(A or B) = P(A) + P(B) - P(A and B)

In this discussion, when we say "A or B occurs" we include three possibilities:

1. A occurs and B does not occur
2. B occurs and A does not occur
3. Both A and B occur

This use of the word "or" is technically called inclusive or because it includes the case in which both A and B occur. If we included only the first two cases, then we would be using an exclusive or.

(Optional) We can derive the law for P(A-or-B) from our law about P(A-and-B). The event "A-or-B" can happen in any of the following ways:

1. A-and-B happens
2. A-and-not-B happens
3. not-A-and-B happens.

The simple event A can happen if either A-and-B happens or A-and-not-B happens. Similarly, the simple event B happens if either A-and-B happens or not-A-and-B happens. P(A) + P(B) is therefore P(A-and-B) + P(A-and-not-B) + P(A-and-B) + P(not-A-and-B), whereas P(A-or-B) is P(A-and-B) + P(A-and-not-B) + P(not-A-and-B). We can make these two sums equal by subtracting one occurrence of P(A-and-B) from the first. Hence, P(A-or-B) = P(A) + P(B) - P(A-and-B).

Now for some examples. If you flip a coin two times, what is the probability that you will get a head on the first flip or a head on the second flip (or both)? Letting Event A be a head on the first flip and Event B be a head on the second flip, then P(A) = 1/2, P(B) = 1/2, and P(A and B) = 1/4. Therefore,

P(A or B) = 1/2 + 1/2 - 1/4 = 3/4.

If you throw a six-sided die and then flip a coin, what is the probability that you will get either a 6 on the die or a head on the coin flip (or both)? Using the formula,

P(6 or head) = P(6) + P(head) - P(6 and head)
             = (1/6) + (1/2) - (1/6)(1/2)
             = 7/12

An alternate approach to computing this value is to start by computing the probability of not getting either a 6 or a head. Then subtract this value from 1 to compute the probability of getting a 6 or a head. Although this is a complicated method, it has the advantage of being applicable to problems with more than two events. Here is the calculation in the present case. The probability of not getting either a 6 or a head can be recast as the probability of

(not getting a 6) AND (not getting a head).

This follows because if you did not get a 6 and you did not get a head, then you did not get a 6 or a head. The probability of not getting a six is 1 - 1/6 = 5/6. The probability of not getting a head is 1 - 1/2 = 1/2. The probability of not getting a six and not getting a head is 5/6 x 1/2 = 5/12. This is therefore the probability of not getting a 6 or a head. The probability of getting a six or a head is therefore (once again) 1 - 5/12 = 7/12.

If you throw a die three times, what is the probability that one or more of your throws will come up with a 1? That is, what is the probability of getting a 1 on the first throw OR a 1 on the second throw OR a 1 on the third throw? The easiest way to approach this problem is to compute the probability of

NOT getting a 1 on the first throw
AND not getting a 1 on the second throw
AND not getting a 1 on the third throw.

The answer will be 1 minus this probability. The probability of not getting a 1 on any of the three throws is 5/6 x 5/6 x 5/6 = 125/216. Therefore, the probability of getting a 1 on at least one of the throws is 1 - 125/216 = 91/216.

Conditional Probabilities

Often it is required to compute the probability of an event given that another event has occurred. For example, what is the probability that two cards drawn at random from a deck of playing cards will both be aces? It might seem that you could use the formula for the probability of two independent events and simply multiply 4/52 x 4/52 = 1/169. This would be incorrect, however, because the two events are not independent. If the first card drawn is an ace, then the probability that the second card is also an ace would be lower because there would only be three aces left in the deck.

Once the first card chosen is an ace, the probability that the second card chosen is also an ace is called the conditional probability of drawing an ace. In this case, the "condition" is that the first card is an ace. Symbolically, we write this as:

P(ace on second draw | an ace on the first draw)

The vertical bar "|" is read as "given," so the above expression is short for: "The probability that an ace is drawn on the second draw given that an ace was drawn on the first draw." What is this probability? Since after an ace is drawn on the first draw, there are 3 aces out of 51 total cards left. This means that the probability that one of these aces will be drawn is 3/51 = 1/17.

If Events A and B are not independent, then P(A and B) = P(A) x P(B|A).

Applying this to the problem of two aces, the probability of drawing two aces from a deck is 4/52 x 3/51 = 1/221.

One more example: If you draw two cards from a deck, what is the probability that you will get the Ace of Diamonds and a black card? There are two ways you can satisfy this condition: (a) You can get the Ace of Diamonds first and then a black card or (b) you can get a black card first and then the Ace of Diamonds. Let's calculate Case A. The probability that the first card is the Ace of Diamonds is 1/52. The probability that the second card is black given that the first card is the Ace of Diamonds is 26/51 because 26 of the remaining 51 cards are black. The probability is therefore 1/52 x 26/51 = 1/102. Now for Case B: the probability that the first card is black is 26/52 = 1/2. The probability that the second card is the Ace of Diamonds given that the first card is black is 1/51. The probability of Case B is therefore 1/2 x 1/51 = 1/102, the same as the probability of Case A. Recall that the probability of A or B is P(A) + P(B) - P(A and B). In this problem, P(A and B) = 0 since a card cannot be the Ace of Diamonds and be a black card. Therefore, the probability of Case A or Case B is 1/102 + 1/102 = 2/102 = 1/51. So, 1/51 is the probability that you will get the Ace of Diamonds and a black card when drawing two cards from a deck.

Birthday Problem

If there are 25 people in a room, what is the probability that at least two of them share the same birthday. If your first thought is that it is 25/365 = 0.068, you will be surprised to learn it is much higher than that. This problem requires the application of the sections on P(A and B) and conditional probability.

This problem is best approached by asking what is the probability that no two people have the same birthday. Once we know this probability, we can simply subtract it from 1 to find the probability that two people share a birthday.

If we choose two people at random, what is the probability that they do not share a birthday? Of the 365 days on which the second person could have a birthday, 364 of them are different from the first person's birthday. Therefore the probability is 364/365. Let's define P2 as the probability that the second person drawn does not share a birthday with the person drawn previously. P2 is therefore 364/365. Now define P3 as the probability that the third person drawn does not share a birthday with anyone drawn previously given that there are no previous birthday matches. P3 is therefore a conditional probability. If there are no previous birthday matches, then two of the 365 days have been "used up," leaving 363 non-matching days. Therefore P3 = 363/365. In like manner, P4 = 362/365, P5 = 361/365, and so on up to P25 = 341/365.

In order for there to be no matches, the second person must not match any previous person and the third person must not match any previous person, andthe fourth person must not match any previous person, etc. Since P(A and B) = P(A)P(B), all we have to do is multiply P2, P3, P4 ...P25 together. The result is 0.431. Therefore the probability of at least one match is 0.569.

Gambler's Fallacy

A fair coin is flipped five times and comes up heads each time. What is the probability that it will come up heads on the sixth flip? The correct answer is, of course, 1/2. But many people believe that a tail is more likely to occur after throwing five heads. Their faulty reasoning may go something like this: "In the long run, the number of heads and tails will be the same, so the tails have some catching up to do." The flaws in this logic are exposed in the simulation in this chapter.

Random Variable

The outcome of an experiment need not be a number, for example, the outcome when a coin is tossed can be 'heads' or 'tails'. However, we often want to represent outcomes as numbers. A random variable is a function that associates a unique numerical value with every outcome of an experiment. The value of the random variable will vary from trial to trial as the experiment is repeated.

There are two types of random variable - discrete and continuous.

A random variable has either an associated probability distribution (discrete random variable) or probability density function (continuous random variable).

Examples

1. A coin is tossed ten times. The random variable X is the number of tails that are noted. X can only take the values 0, 1, ..., 10, so X is a discrete random variable.
2. A light bulb is burned until it burns out. The random variable Y is its lifetime in hours. Y can take any positive real value, so Y is a continuous random variable.

Expected Value 

                               The expected value (or population mean) of a random variable indicates its average or central value. It is a useful summary value (a number) of the variable's distribution.

Stating the expected value gives a general impression of the behaviour of some random variable without giving full details of its probability distribution (if it is discrete) or its probability density function (if it is continuous).

Two random variables with the same expected value can have very different distributions. There are other useful descriptive measures which affect the shape of the distribution, for example variance.

The expected value of a random variable X is symbolised by E(X) or µ.

If X is a discrete random variable with possible values x1, x2, x3, ..., xn, and p(xi) denotes P(X = xi), then the expected value of X is defined by:

where the elements are summed over all values of the random variable X.

If X is a continuous random variable with probability density function f(x), then the expected value of X is defined by:

Example

Discrete case : When a die is thrown, each of the possible faces 1, 2, 3, 4, 5, 6 (the xi's) has a probability of 1/6 (the p(xi)'s) of showing. The expected value of the face showing is therefore:

µ = E(X) = (1 x 1/6) + (2 x 1/6) + (3 x 1/6) + (4 x 1/6) + (5 x 1/6) + (6 x 1/6) = 3.5

Notice that, in this case, E(X) is 3.5, which is not a possible value of X.

 Variance 

                         The (population) variance of a random variable is a non-negative number which gives an idea of how widely spread the values of the random variable are likely to be; the larger the variance, the more scattered the observations on average.

Stating the variance gives an impression of how closely concentrated round the expected value the distribution is; it is a measure of the 'spread' of a distribution about its average value.

Variance is symbolised by V(X) or Var(X) or 

The variance of the random variable X is defined to be:

where E(X) is the expected value of the random variable X.

Notes

1. the larger the variance, the further that individual values of the random variable (observations) tend to be from the mean, on average;
2. the smaller the variance, the closer that individual values of the random variable (observations) tend to be to the mean, on average;

3. taking the square root of the variance gives the standard deviation, i.e.:

   

4. the variance and standard deviation of a random variable are always non-negative.

 Probability Distribution

                     The probability distribution of a discrete random variable is a list of probabilities associated with each of its possible values. It is also sometimes called the probability function or the probability mass function.

More formally, the probability distribution of a discrete random variable X is a function which gives the probability p(xi) that the random variable equals xi, for each value xi:

p(xi) = P(X=xi)

It satisfies the following conditions:

1. 
2. 

 Cumulative Distribution Function

                                                 All random variables (discrete and continuous) have a cumulative distribution function. It is a function giving the probability that the random variable X is less than or equal to x, for every value x.

Formally, the cumulative distribution function F(x) is defined to be:

for

For a discrete random variable, the cumulative distribution function is found by summing up the probabilities as in the example below.

For a continuous random variable, the cumulative distribution function is the integral of its probability density function.

Example

Discrete case : Suppose a random variable X has the following probability distribution p(xi):

xi		0	1	2	3	4	5
p(xi)		1/32	5/32	10/32	10/32	5/32	1/32

This is actually a binomial distribution: Bi(5, 0.5) or B(5, 0.5). The cumulative distribution function F(x) is then:

xi		0	1	2	3	4	5
F(xi)		1/32	6/32	16/32	26/32	31/32	32/32

F(x) does not change at intermediate values. For example:

F(1.3) = F(1) = 6/32

F(2.86) = F(2) = 16/32

 Probability Density Function

                                                    The probability density function of a continuous random variable is a function which can be integrated to obtain the probability that the random variable takes a value in a given interval.

More formally, the probability density function, f(x), of a continuous random variable X is the derivative of the cumulative distribution function F(x):

Since  it follows that:

If f(x) is a probability density function then it must obey two conditions:

1. that the total probability for all possible values of the continuous random variable X is 1:

   

2. that the probability density function can never be negative: f(x) > 0 for all x.

 Discrete Random Variable

                                           A discrete random variable is one which may take on only a countable number of distinct values such as 0, 1, 2, 3, 4, ... Discrete random variables are usually (but not necessarily) counts. If a random variable can take only a finite number of distinct values, then it must be discrete. Examples of discrete random variables include the number of children in a family, the Friday night attendance at a cinema, the number of patients in a doctor's surgery, the number of defective light bulbs in a box of ten.

Compare continuous random variable.

Continuous Random Variable

                                                   A continuous random variable is one which takes an infinite number of possible values. Continuous random variables are usually measurements. Examples include height, weight, the amount of sugar in an orange, the time required to run a mile.

Compare discrete random variable.

 Independent Random Variables

                                                                 Two random variables X and Y say, are said to be independent if and only if the value of X has no influence on the value of Y and vice versa.

The cumulative distribution functions of two independent random variables X and Y are related by

F(x,y) = G(x).H(y)

where

G(x) and H(y) are the marginal distribution functions of X and Y for all pairs (x,y).

Knowledge of the value of X does not effect the probability distribution of Y and vice versa. Thus there is no relationship between the values of independent random variables.

For continuous independent random variables, their probability density functions are related by

f(x,y) = g(x).h(y)

where

g(x) and h(y) are the marginal density functions of the random variables X and Y respectively, for all pairs (x,y).

For discrete independent random variables, their probabilities are related by

P(X = xi ; Y = yj) = P(X = xi).P(Y=yj)

for each pair (xi,yj).

Probability-Probability (P-P) Plot

                                 A probability-probability (P-P) plot is used to see if a given set of data follows some specified distribution. It should be approximately linear if the specified distribution is the correct model.

The probability-probability (P-P) plot is constructed using the theoretical cumulative distribution function, F(x), of the specified model. The values in the sample of data, in order from smallest to largest, are denoted x(1), x(2), ..., x(n). For i = 1, 2, ....., n, F(x(i)) is plotted against (i-0.5)/n.

Compare quantile-quantile (Q-Q) plot.

Quantile-Quantile (QQ) Ploth

                                                            quantile-quantile (Q-Q) plot is used to see if a given set of data follows some specified distribution. It should be approximately linear if the specified distribution is the correct model.

The quantile-quantile (Q-Q) plot is constructed using the theoretical cumulative distribution function, F(x), of the specified model. The values in the sample of data, in order from smallest to largest, are denoted x(1), x(2), ..., x(n). For i = 1, 2, ....., n, x(i) is plotted against F^-1((i-0.5)/n).

Compare probability-probability (P-P) plot.

Normal Distribution

Normal distributions model (some) continuous random variables. Strictly, a Normal random variable should be capable of assuming any value on the real line, though this requirement is often waived in practice. For example, height at a given age for a given gender in a given racial group is adequately described by a Normal random variable even though heights must be positive.

A continuous random variable X, taking all real values in the range  is said to follow a Normal distribution with parameters µ and  if it has probability density function

We write

This probability density function (p.d.f.) is a symmetrical, bell-shaped curve, centred at its expected value µ. The variance is .

Many distributions arising in practice can be approximated by a Normal distribution. Other random variables may be transformed to normality.

The simplest case of the normal distribution, known as the Standard Normal Distribution, has expected value zero and variance one. This is written as N(0,1).

Examples

  

Poisson Distribution

Poisson distributions model (some) discrete random variables. Typically, a Poisson random variable is a count of the number of events that occur in a certain time interval or spatial area. For example, the number of cars passing a fixed point in a 5 minute interval, or the number of calls received by a switchboard during a given period of time.

A discrete random variable X is said to follow a Poisson distribution with parameter m, written X ~ Po(m), if it has probability distribution

where

x = 0, 1, 2, ..., n

m > 0.

The following requirements must be met:

1. the length of the observation period is fixed in advance;
2. the events occur at a constant average rate;
3. the number of events occurring in disjoint intervals are statistically independent.

The Poisson distribution has expected value E(X) = m and variance V(X) = m; i.e. E(X) = V(X) = m.

The Poisson distribution can sometimes be used to approximate the Binomial distribution with parameters n and p. When the number of observations n is large, and the success probability p is small, the Bi(n,p) distribution approaches the Poisson distribution with the parameter given by m = np. This is useful since the computations involved in calculating binomial probabilities are greatly reduced.

Examples

 

Binomial Distribution

Binomial distributions model (some) discrete random variables.

Typically, a binomial random variable is the number of successes in a series of trials, for example, the number of 'heads' occurring when a coin is tossed 50 times.

A discrete random variable X is said to follow a Binomial distribution with parameters n and p, written X ~ Bi(n,p) or X ~ B(n,p), if it has probability distribution

where

x = 0, 1, 2, ......., n

n = 1, 2, 3, .......

p = success probability; 0 < p < 1

The trials must meet the following requirements:

1. the total number of trials is fixed in advance;
2. there are just two outcomes of each trial; success and failure;
3. the outcomes of all the trials are statistically independent;
4. all the trials have the same probability of success.

The Binomial distribution has expected value E(X) = np and variance V(X) = np(1-p).

Examples

 

Geometric Distribution

Geometric distributions model (some) discrete random variables. Typically, a Geometric random variable is the number of trials required to obtain the first failure, for example, the number of tosses of a coin untill the first 'tail' is obtained, or a process where components from a production line are tested, in turn, until the first defective item is found.

A discrete random variable X is said to follow a Geometric distribution with parameter p, written X ~ Ge(p), if it has probability distribution

P(X=x) = p^x-1(1-p)^x

where

x = 1, 2, 3, ...

p = success probability; 0 < p < 1

The trials must meet the following requirements:

1. the total number of trials is potentially infinite;
2. there are just two outcomes of each trial; success and failure;
3. the outcomes of all the trials are statistically independent;
4. all the trials have the same probability of success.

The Geometric distribution has expected value E(X)= 1/(1-p) and variance V(X)=p/{(1-p)²}.

The Geometric distribution is related to the Binomial distribution in that both are based on independent trials in which the probability of success is constant and equal to p. However, a Geometric random variable is the number of trials until the first failure, whereas a Binomial random variable is the number of successes in n trials.

Examples

 

Uniform Distribution

Uniform distributions model (some) continuous random variables and (some) discrete random variables. The values of a uniform random variable are uniformly distributed over an interval. For example, if buses arrive at a given bus stop every 15 minutes, and you arrive at the bus stop at a random time, the time you wait for the next bus to arrive could be described by a uniform distribution over the interval from 0 to 15.

A discrete random variable X is said to follow a Uniform distribution with parameters a and b, written X ~ Un(a,b), if it has probability distribution

P(X=x) = 1/(b-a)

where

x = 1, 2, 3, ......., n.

A discrete uniform distribution has equal probability at each of its n values.

A continuous random variable X is said to follow a Uniform distribution with parameters a and b, written X ~ Un(a,b), if its probability density function is constant within a finite interval [a,b], and zero outside this interval (with a less than or equal to b).

The Uniform distribution has expected value E(X)=(a+b)/2 and variance {(b-a)²}/12.

Example

Central Limit Theorem

The Central Limit Theorem states that whenever a random sample of size n is taken from any distribution with mean µ and variance , then the sample mean  will be approximately normally distributed with mean µ and variance /n. The larger the value of the sample size n, the better the approximation to the normal.

This is very useful when it comes to inference. For example, it allows us (if the sample size is fairly large) to use hypothesis tests which assume normality even if our data appear non-normal. This is because the tests use the sample mean , which the Central Limit Theorem tells us will be approximately normally distributed.