The internal rate of return (IRR) is a rate of return used in capital budgeting to measure and compare the profitability of investments. It is also called the discounted cash flow rate of return (DCFROR) or simply the rate of return (ROR). In the context of savings and loans the IRR is also called the effective interest rate. The term internal refers to the fact that its calculation does not incorporate environmental factors (e.g., the interest rate or inflation).
The internal rate of return on an investment or project is the "annualized effective compounded return rate" or discount rate that makes the net present value of all cash flows (both positive and negative) from a particular investment equal to zero.
In more specific terms, the IRR of an investment is the interest rate at which the net present value of costs (negative cash flows) of the investment equals the net present value of the benefits (positive cash flows) of the investment.
Internal rates of return are commonly used to evaluate the desirability of investments or projects. The higher a project's internal rate of return, the more desirable it is to undertake the project. Assuming all other factors are equal among the various projects, the project with the highest IRR would probably be considered the best and undertaken first.
A firm (or individual) should, in theory, undertake all projects or investments available with IRRs that exceed the cost of capital. Investment may be limited by availability of funds to the firm and/or by the firm's capacity or ability to manage numerous projects.
An investment is considered acceptable if its internal rate of return is greater than an established minimum acceptable rate of return or cost of capital. In a scenario where an investment is considered by a firm that has equity holders, this minimum rate is the cost of capital of the investment (which may be determined by the risk-adjusted cost of capital of alternative investments). This ensures that the investment is supported by equity holders since, in general, an investment whose IRR exceeds its cost of capital adds value for the company (i.e., it is economically profitable).
Given the (period, cash flow) pairs ( ,
,  ) where
) where  is a positive integer, the total number of periods
is a positive integer, the total number of periods  , and the net present value
, and the net present value  , the internal rate of return is given by
, the internal rate of return is given by  in:
in:
 is calculated using the period in which the majority of the problem is
defined (e.g., using months if most of the cash flows occur at monthly
intervals) and converted to a yearly period thereafter.
is calculated using the period in which the majority of the problem is
defined (e.g., using months if most of the cash flows occur at monthly
intervals) and converted to a yearly period thereafter.
Any fixed time can be used in place of the present (e.g., the end of one interval of an annuity); the value obtained is zero if and only if the NPV is zero.
In the case that the cash flows are random variables, such as in the case of a life annuity, the expected values are put into the above formula.
Often, the value of cannot be found analytically. In this case, numerical methods or graphical methods must be used.
cannot be found analytically. In this case, numerical methods or graphical methods must be used.
then the IRR is given by
is given by
 , there are many numerical methods that can be used to estimate
, there are many numerical methods that can be used to estimate  . For example, using the secant method,
. For example, using the secant method,  is given by
is given by
 is considered the
is considered the  th approximation of the IRR.
th approximation of the IRR.
This can be found to an arbitrary degree of accuracy. An accuracy of 0.00001% is provided by Microsoft Excel.
can be found to an arbitrary degree of accuracy. An accuracy of 0.00001% is provided by Microsoft Excel.
The convergence behaviour of the sequence is governed by the following:
 when
when  or
or  when
when  may speed up convergence of
may speed up convergence of 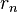 to
to  .
.
Given two estimates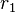 and
and  for IRR, the secant method equation (see above) with
for IRR, the secant method equation (see above) with 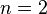 will always produce an improved estimate
will always produce an improved estimate  .
This is sometimes referred to as the Hit and Trial (or Trial and Error)
method. More accurate interpolation formulas can also be obtained: for
instance the secant formula with correction
.
This is sometimes referred to as the Hit and Trial (or Trial and Error)
method. More accurate interpolation formulas can also be obtained: for
instance the secant formula with correction
 )
has been shown to be almost 10 times more accurate than the secant
formula for a wide range of interest rates and initial guesses. For
example, using the stream of payments {−4000, 1200, 1410, 1875, 1050}
and initial guesses
)
has been shown to be almost 10 times more accurate than the secant
formula for a wide range of interest rates and initial guesses. For
example, using the stream of payments {−4000, 1200, 1410, 1875, 1050}
and initial guesses  and
and  the secant formula with correction gives an IRR estimate of 14.2% (0.7%
error) as compared to IRR = 13.2% (7% error) from the secant method.
Other improved formulas may be found in [2]
the secant formula with correction gives an IRR estimate of 14.2% (0.7%
error) as compared to IRR = 13.2% (7% error) from the secant method.
Other improved formulas may be found in [2]
If applied iteratively, either the secant method or the improved formula will always converge to the correct solution.
Both the secant method and the improved formula rely on initial guesses for IRR. The following initial guesses may be used:
If the IRR is less than the cost of capital, reject the project.
In cases where one project has a higher initial investment than a
second mutually exclusive project, the first project may have a lower
IRR (expected return), but a higher NPV (increase in shareholders'
wealth) and should thus be accepted over the second project (assuming no
capital constraints).
IRR assumes reinvestment of interim cash flows in projects with equal rates of return (the reinvestment can be the same project or a different project). Therefore, IRR overstates the annual equivalent rate of return for a project whose interim cash flows are reinvested at a rate lower than the calculated IRR. This presents a problem, especially for high IRR projects, since there is frequently not another project available in the interim that can earn the same rate of return as the first project.
Since IRR does not consider cost of capital, it should not be used to compare projects of different duration. Modified Internal Rate of Return (MIRR) does consider cost of capital and provides a better indication of a project's efficiency in contributing to the firm's discounted cash flow.
In the case of positive cash flows followed by negative ones and then by positive ones (for example, + + − − − +) the IRR may have multiple values. In this case a discount rate may be used for the borrowing cash flow and the IRR calculated for the investment cash flow. This applies for example when a customer makes a deposit before a specific machine is built.
In a series of cash flows like (−10, 21, −11), one initially invests money, so a high rate of return is best, but then receives more than one possesses, so then one owes money, so now a low rate of return is best. In this case it is not even clear whether a high or a low IRR is better. There may even be multiple IRRs for a single project, like in the example 0% as well as 10%. Examples of this type of project are strip mines and nuclear power plants, where there is usually a large cash outflow at the end of the project.
In general, the IRR can be calculated by solving a polynomial equation. Sturm's theorem can be used to determine if that equation has a unique real solution. In general the IRR equation cannot be solved analytically but only iteratively.
When a project has multiple IRRs it may be more convenient to compute the IRR of the project with the benefits reinvested. Accordingly, MIRR is used, which has an assumed reinvestment rate, usually equal to the project's cost of capital.
It has been shown that with multiple internal rates of return, the IRR approach can still be interpreted in a way that is consistent with the present value approach provided that the underlying investment stream is correctly identified as net investment or net borrowing.
See also for a way of identifying the relevant value of the IRR from a set of multiple IRR solutions.
Despite a strong academic preference for NPV, surveys indicate that executives prefer IRR over NPV.Apparently, managers find it easier to compare investments of different sizes in terms of percentage rates of return than by dollars of NPV. However, NPV remains the "more accurate" reflection of value to the business. IRR, as a measure of investment efficiency may give better insights in capital constrained situations. However, when comparing mutually exclusive projects, NPV is the appropriate measure.
Thus, internal rate(s) of return follow from the net present value as a function of the rate of return. This function is continuous. Towards a rate of return of −100% the net present value approaches infinity with the sign of the last cash flow, and towards a rate of return of positive infinity the net present value approaches the first cash flow (the one at the present). Therefore, if the first and last cash flow have a different sign there exists an internal rate of return. Examples of time series without an IRR:
Similarly, in the case of a series of exclusively positive cash flows followed by a series of exclusively negative ones the IRR is also unique.
Finally, by Descartes' rule of signs, the number of internal rates of return can never be more than the number of changes in sign of cash flow.
The internal rate of return on an investment or project is the "annualized effective compounded return rate" or discount rate that makes the net present value of all cash flows (both positive and negative) from a particular investment equal to zero.
In more specific terms, the IRR of an investment is the interest rate at which the net present value of costs (negative cash flows) of the investment equals the net present value of the benefits (positive cash flows) of the investment.
Internal rates of return are commonly used to evaluate the desirability of investments or projects. The higher a project's internal rate of return, the more desirable it is to undertake the project. Assuming all other factors are equal among the various projects, the project with the highest IRR would probably be considered the best and undertaken first.
A firm (or individual) should, in theory, undertake all projects or investments available with IRRs that exceed the cost of capital. Investment may be limited by availability of funds to the firm and/or by the firm's capacity or ability to manage numerous projects.
Uses
Important: Because the internal rate of return is a rate quantity, it is an indicator of the efficiency, quality, or yield of an investment. This is in contrast with the net present value, which is an indicator of the value or magnitude of an investment.An investment is considered acceptable if its internal rate of return is greater than an established minimum acceptable rate of return or cost of capital. In a scenario where an investment is considered by a firm that has equity holders, this minimum rate is the cost of capital of the investment (which may be determined by the risk-adjusted cost of capital of alternative investments). This ensures that the investment is supported by equity holders since, in general, an investment whose IRR exceeds its cost of capital adds value for the company (i.e., it is economically profitable).
Calculation
Given a collection of pairs (time, cash flow) involved in a project, the internal rate of return follows from the net present value as a function of the rate of return. A rate of return for which this function is zero is an internal rate of return.Given the (period, cash flow) pairs (
 ,
, 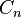 ) where
) where  is a positive integer, the total number of periods
is a positive integer, the total number of periods  , and the net present value
, and the net present value 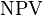 , the internal rate of return is given by
, the internal rate of return is given by  in:
in: is calculated using the period in which the majority of the problem is
defined (e.g., using months if most of the cash flows occur at monthly
intervals) and converted to a yearly period thereafter.
is calculated using the period in which the majority of the problem is
defined (e.g., using months if most of the cash flows occur at monthly
intervals) and converted to a yearly period thereafter.Any fixed time can be used in place of the present (e.g., the end of one interval of an annuity); the value obtained is zero if and only if the NPV is zero.
In the case that the cash flows are random variables, such as in the case of a life annuity, the expected values are put into the above formula.
Often, the value of
 cannot be found analytically. In this case, numerical methods or graphical methods must be used.
cannot be found analytically. In this case, numerical methods or graphical methods must be used.Example
If an investment may be given by the sequence of cash flowsYear ( ) ) |
Cash flow (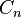 ) ) |
|---|---|
| 0 | -123400 |
| 1 | 36200 |
| 2 | 54800 |
| 3 | 48100 |
then the IRR
 is given by
is given byNumerical solution
Since the above is a manifestation of the general problem of finding the roots of the equation , there are many numerical methods that can be used to estimate
, there are many numerical methods that can be used to estimate  . For example, using the secant method,
. For example, using the secant method,  is given by
is given by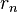 is considered the
is considered the  th approximation of the IRR.
th approximation of the IRR.This
 can be found to an arbitrary degree of accuracy. An accuracy of 0.00001% is provided by Microsoft Excel.
can be found to an arbitrary degree of accuracy. An accuracy of 0.00001% is provided by Microsoft Excel.The convergence behaviour of the sequence is governed by the following:
- If the function
 has a single real root
has a single real root  , then the sequence will converge reproducibly towards
, then the sequence will converge reproducibly towards  .
. - If the function
 has
has  real roots
real roots  ,
then the sequence will converge to one of the roots and changing the
values of the initial pairs may change the root to which it converges.
,
then the sequence will converge to one of the roots and changing the
values of the initial pairs may change the root to which it converges. - If function
 has no real roots, then the sequence will tend towards +∞.
has no real roots, then the sequence will tend towards +∞.
 when
when  or
or  when
when  may speed up convergence of
may speed up convergence of 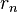 to
to  .
.Numerical solution for single outflow and multiple inflows
Of particular interest is the case where the stream of payments consists of a single outflow, followed by multiple inflows occurring at equal periods. In the above notation, this corresponds to:Given two estimates
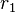 and
and  for IRR, the secant method equation (see above) with
for IRR, the secant method equation (see above) with 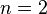 will always produce an improved estimate
will always produce an improved estimate  .
This is sometimes referred to as the Hit and Trial (or Trial and Error)
method. More accurate interpolation formulas can also be obtained: for
instance the secant formula with correction
.
This is sometimes referred to as the Hit and Trial (or Trial and Error)
method. More accurate interpolation formulas can also be obtained: for
instance the secant formula with correction ,
,
 )
has been shown to be almost 10 times more accurate than the secant
formula for a wide range of interest rates and initial guesses. For
example, using the stream of payments {−4000, 1200, 1410, 1875, 1050}
and initial guesses
)
has been shown to be almost 10 times more accurate than the secant
formula for a wide range of interest rates and initial guesses. For
example, using the stream of payments {−4000, 1200, 1410, 1875, 1050}
and initial guesses  and
and  the secant formula with correction gives an IRR estimate of 14.2% (0.7%
error) as compared to IRR = 13.2% (7% error) from the secant method.
Other improved formulas may be found in [2]
the secant formula with correction gives an IRR estimate of 14.2% (0.7%
error) as compared to IRR = 13.2% (7% error) from the secant method.
Other improved formulas may be found in [2]If applied iteratively, either the secant method or the improved formula will always converge to the correct solution.
Both the secant method and the improved formula rely on initial guesses for IRR. The following initial guesses may be used:
Decision criterion
If the IRR is greater than the cost of capital, accept the project.If the IRR is less than the cost of capital, reject the project.
Problems with using internal rate of return
As an investment decision tool, the calculated IRR should not be used to rate mutually exclusive projects, but only to decide whether a single project is worth investing in.IRR assumes reinvestment of interim cash flows in projects with equal rates of return (the reinvestment can be the same project or a different project). Therefore, IRR overstates the annual equivalent rate of return for a project whose interim cash flows are reinvested at a rate lower than the calculated IRR. This presents a problem, especially for high IRR projects, since there is frequently not another project available in the interim that can earn the same rate of return as the first project.
When the calculated IRR is higher than the true reinvestment rate for interim cash flows, the measure will overestimate — sometimes very significantly — the annual equivalent return from the project. The formula assumes that the company has additional projects, with equally attractive prospects, in which to invest the interim cash flows.This makes IRR a suitable (and popular) choice for analyzing venture capital and other private equity investments, as these strategies usually require several cash investments throughout the project, but only see one cash outflow at the end of the project (e.g., via IPO or M&A).
Since IRR does not consider cost of capital, it should not be used to compare projects of different duration. Modified Internal Rate of Return (MIRR) does consider cost of capital and provides a better indication of a project's efficiency in contributing to the firm's discounted cash flow.
In the case of positive cash flows followed by negative ones and then by positive ones (for example, + + − − − +) the IRR may have multiple values. In this case a discount rate may be used for the borrowing cash flow and the IRR calculated for the investment cash flow. This applies for example when a customer makes a deposit before a specific machine is built.
In a series of cash flows like (−10, 21, −11), one initially invests money, so a high rate of return is best, but then receives more than one possesses, so then one owes money, so now a low rate of return is best. In this case it is not even clear whether a high or a low IRR is better. There may even be multiple IRRs for a single project, like in the example 0% as well as 10%. Examples of this type of project are strip mines and nuclear power plants, where there is usually a large cash outflow at the end of the project.
In general, the IRR can be calculated by solving a polynomial equation. Sturm's theorem can be used to determine if that equation has a unique real solution. In general the IRR equation cannot be solved analytically but only iteratively.
When a project has multiple IRRs it may be more convenient to compute the IRR of the project with the benefits reinvested. Accordingly, MIRR is used, which has an assumed reinvestment rate, usually equal to the project's cost of capital.
It has been shown that with multiple internal rates of return, the IRR approach can still be interpreted in a way that is consistent with the present value approach provided that the underlying investment stream is correctly identified as net investment or net borrowing.
See also for a way of identifying the relevant value of the IRR from a set of multiple IRR solutions.
Despite a strong academic preference for NPV, surveys indicate that executives prefer IRR over NPV.Apparently, managers find it easier to compare investments of different sizes in terms of percentage rates of return than by dollars of NPV. However, NPV remains the "more accurate" reflection of value to the business. IRR, as a measure of investment efficiency may give better insights in capital constrained situations. However, when comparing mutually exclusive projects, NPV is the appropriate measure.
Mathematics
Mathematically, the value of the investment is assumed to undergo exponential growth or decay according to some rate of return (any value greater than −100%), with discontinuities for cash flows, and the IRR of a series of cash flows is defined as any rate of return that results in a net present value of zero (or equivalently, a rate of return that results in the correct value of zero after the last cash flow).Thus, internal rate(s) of return follow from the net present value as a function of the rate of return. This function is continuous. Towards a rate of return of −100% the net present value approaches infinity with the sign of the last cash flow, and towards a rate of return of positive infinity the net present value approaches the first cash flow (the one at the present). Therefore, if the first and last cash flow have a different sign there exists an internal rate of return. Examples of time series without an IRR:
- Only negative cash flows — the NPV is negative for every rate of return.
- (−1, 1, −1), rather small positive cash flow between two negative cash flows; the NPV is a quadratic function of 1/(1 + r), where r is the rate of return, or put differently, a quadratic function of the discount rate r/(1 + r); the highest NPV is −0.75, for r = 100%.
Similarly, in the case of a series of exclusively positive cash flows followed by a series of exclusively negative ones the IRR is also unique.
Finally, by Descartes' rule of signs, the number of internal rates of return can never be more than the number of changes in sign of cash flow.