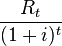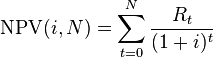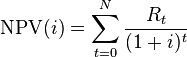In finance, the net present value (NPV) or net present worth (NPW) of a time series of cash flows, both incoming and outgoing, is defined as the sum of the present values (PVs) of the individual cash flows of the same entity.
In the case when all future cash flows are incoming (such as coupons and principal of a bond) and the only outflow of cash is the purchase price, the NPV is simply the PV of future cash flows minus the purchase price (which is its own PV). NPV is a central tool in discounted cash flow (DCF) analysis and is a standard method for using the time value of money to appraise long-term projects. Used for capital budgeting and widely used throughout economics, finance, and accounting, it measures the excess or shortfall of cash flows, in present value terms, above the cost of funds.
NPV can be described as the “difference amount” between the sums of discounted: cash inflows and cash outflows. It compares the present value of money today to the present value of money in the future, taking inflation and returns into account
The NPV of a sequence of cash flows takes as input the cash flows and a discount rate or discount curve and outputs a price; the converse process in DCF analysis — taking a sequence of cash flows and a price as input and inferring as output a discount rate (the discount rate which would yield the given price as NPV) — is called the yield and is more widely used in bond trading.
Given the (period, cash flow) pairs ( ,
, 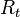 ) where
) where  is the total number of periods, the net present value
is the total number of periods, the net present value 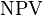 is given by:
is given by:
A firm's weighted average cost of capital (after tax) is often used, but many people believe that it is appropriate to use higher discount rates to adjust for risk, opportunity cost, or other factors. A variable discount rate with higher rates applied to cash flows occurring further along the time span might be used to reflect the yield curve premium for long-term debt.
Another approach to choosing the discount rate factor is to decide the rate which the capital needed for the project could return if invested in an alternative venture. If, for example, the capital required for Project A can earn 5% elsewhere, use this discount rate in the NPV calculation to allow a direct comparison to be made between Project A and the alternative. Related to this concept is to use the firm's reinvestment rate. Reinvestment rate can be defined as the rate of return for the firm's investments on average. When analyzing projects in a capital constrained environment, it may be appropriate to use the reinvestment rate rather than the firm's weighted average cost of capital as the discount factor. It reflects opportunity cost of investment, rather than the possibly lower cost of capital.
An NPV calculated using variable discount rates (if they are known for the duration of the investment) may better reflect the situation than one calculated from a constant discount rate for the entire investment duration. Refer to the tutorial article written by Samuel Baker for more detailed relationship between the NPV value and the discount rate.
For some professional investors, their investment funds are committed to target a specified rate of return. In such cases, that rate of return should be selected as the discount rate for the NPV calculation. In this way, a direct comparison can be made between the profitability of the project and the desired rate of return.
To some extent, the selection of the discount rate is dependent on the use to which it will be put. If the intent is simply to determine whether a project will add value to the company, using the firm's weighted average cost of capital may be appropriate. If trying to decide between alternative investments in order to maximize the value of the firm, the corporate reinvestment rate would probably be a better choice.
Using variable rates over time, or discounting "guaranteed" cash flows differently from "at risk" cash flows, may be a superior methodology but is seldom used in practice. Using the discount rate to adjust for risk is often difficult to do in practice (especially internationally) and is difficult to do well. An alternative to using discount factor to adjust for risk is to explicitly correct the cash flows for the risk elements using rNPV or a similar method, then discount at the firm's rate.
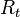 is a positive value, the project is in the status of positive cash inflow in the time of t. If
is a positive value, the project is in the status of positive cash inflow in the time of t. If 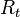 is a negative value, the project is in the status of discounted cash outflow in the time of t.
Appropriately risked projects with a positive NPV could be accepted.
This does not necessarily mean that they should be undertaken since NPV
at the cost of capital may not account for opportunity cost, i.e.,
comparison with other available investments. In financial theory, if
there is a choice between two mutually exclusive alternatives, the one
yielding the higher NPV should be selected.
is a negative value, the project is in the status of discounted cash outflow in the time of t.
Appropriately risked projects with a positive NPV could be accepted.
This does not necessarily mean that they should be undertaken since NPV
at the cost of capital may not account for opportunity cost, i.e.,
comparison with other available investments. In financial theory, if
there is a choice between two mutually exclusive alternatives, the one
yielding the higher NPV should be selected.
The present value (PV) can be calculated for each year:
The sum of all these present values is the net present value, which
equals 65,816.04. Since the NPV is greater than zero, it would be better
to invest in the project than to do nothing, and the corporation should
invest in this project if there is no alternative with a higher NPV.
In the case when all future cash flows are incoming (such as coupons and principal of a bond) and the only outflow of cash is the purchase price, the NPV is simply the PV of future cash flows minus the purchase price (which is its own PV). NPV is a central tool in discounted cash flow (DCF) analysis and is a standard method for using the time value of money to appraise long-term projects. Used for capital budgeting and widely used throughout economics, finance, and accounting, it measures the excess or shortfall of cash flows, in present value terms, above the cost of funds.
NPV can be described as the “difference amount” between the sums of discounted: cash inflows and cash outflows. It compares the present value of money today to the present value of money in the future, taking inflation and returns into account
The NPV of a sequence of cash flows takes as input the cash flows and a discount rate or discount curve and outputs a price; the converse process in DCF analysis — taking a sequence of cash flows and a price as input and inferring as output a discount rate (the discount rate which would yield the given price as NPV) — is called the yield and is more widely used in bond trading.
Formula
Each cash inflow/outflow is discounted back to its present value (PV). Then they are summed. Therefore NPV is the sum of all terms, - the time of the cash flow
- the time of the cash flow - the discount rate (the rate of return that could be earned on an investment in the financial markets with similar risk.); the opportunity cost of capital
- the discount rate (the rate of return that could be earned on an investment in the financial markets with similar risk.); the opportunity cost of capital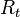 - the net cash flow i.e. cash inflow – cash outflow, at time t . For educational purposes,
- the net cash flow i.e. cash inflow – cash outflow, at time t . For educational purposes,  is commonly placed to the left of the sum to emphasize its role as (minus) the investment.
is commonly placed to the left of the sum to emphasize its role as (minus) the investment.
Given the (period, cash flow) pairs (
 ,
, 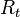 ) where
) where  is the total number of periods, the net present value
is the total number of periods, the net present value 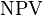 is given by:
is given by:The discount rate
Main article: Discount rate
The rate used to discount future cash flows to the present value is a key variable of this process.A firm's weighted average cost of capital (after tax) is often used, but many people believe that it is appropriate to use higher discount rates to adjust for risk, opportunity cost, or other factors. A variable discount rate with higher rates applied to cash flows occurring further along the time span might be used to reflect the yield curve premium for long-term debt.
Another approach to choosing the discount rate factor is to decide the rate which the capital needed for the project could return if invested in an alternative venture. If, for example, the capital required for Project A can earn 5% elsewhere, use this discount rate in the NPV calculation to allow a direct comparison to be made between Project A and the alternative. Related to this concept is to use the firm's reinvestment rate. Reinvestment rate can be defined as the rate of return for the firm's investments on average. When analyzing projects in a capital constrained environment, it may be appropriate to use the reinvestment rate rather than the firm's weighted average cost of capital as the discount factor. It reflects opportunity cost of investment, rather than the possibly lower cost of capital.
An NPV calculated using variable discount rates (if they are known for the duration of the investment) may better reflect the situation than one calculated from a constant discount rate for the entire investment duration. Refer to the tutorial article written by Samuel Baker for more detailed relationship between the NPV value and the discount rate.
For some professional investors, their investment funds are committed to target a specified rate of return. In such cases, that rate of return should be selected as the discount rate for the NPV calculation. In this way, a direct comparison can be made between the profitability of the project and the desired rate of return.
To some extent, the selection of the discount rate is dependent on the use to which it will be put. If the intent is simply to determine whether a project will add value to the company, using the firm's weighted average cost of capital may be appropriate. If trying to decide between alternative investments in order to maximize the value of the firm, the corporate reinvestment rate would probably be a better choice.
Using variable rates over time, or discounting "guaranteed" cash flows differently from "at risk" cash flows, may be a superior methodology but is seldom used in practice. Using the discount rate to adjust for risk is often difficult to do in practice (especially internationally) and is difficult to do well. An alternative to using discount factor to adjust for risk is to explicitly correct the cash flows for the risk elements using rNPV or a similar method, then discount at the firm's rate.
Use in decision making
NPV is an indicator of how much value an investment or project adds to the firm. With a particular project, if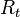 is a positive value, the project is in the status of positive cash inflow in the time of t. If
is a positive value, the project is in the status of positive cash inflow in the time of t. If 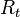 is a negative value, the project is in the status of discounted cash outflow in the time of t.
Appropriately risked projects with a positive NPV could be accepted.
This does not necessarily mean that they should be undertaken since NPV
at the cost of capital may not account for opportunity cost, i.e.,
comparison with other available investments. In financial theory, if
there is a choice between two mutually exclusive alternatives, the one
yielding the higher NPV should be selected.
is a negative value, the project is in the status of discounted cash outflow in the time of t.
Appropriately risked projects with a positive NPV could be accepted.
This does not necessarily mean that they should be undertaken since NPV
at the cost of capital may not account for opportunity cost, i.e.,
comparison with other available investments. In financial theory, if
there is a choice between two mutually exclusive alternatives, the one
yielding the higher NPV should be selected.| If... | It means... | Then... |
|---|---|---|
| NPV > 0 | the investment would add value to the firm | the project may be accepted |
| NPV < 0 | the investment would subtract value from the firm | the project should be rejected |
| NPV = 0 | the investment would neither gain nor lose value for the firm | We should be indifferent in the decision whether to accept or reject the project. This project adds no monetary value. Decision should be based on other criteria, e.g., strategic positioning or other factors not explicitly included in the calculation. |
Interpretation as integral transform
The time-discrete formula of the net present value- r(t) is the rate of flowing cash given in money per time, and r(t) = 0 when the investment is over.
Example
A corporation must decide whether to introduce a new product line. The new product will have start-up expenditures, operational expenditures, and then it will have associated incoming cash receipts (sales) and disbursements (Cash paid for materials, supplies, direct labor, maintenance, repairs, and direct overhead) over 12 years. This project will have an immediate (t=0) cash outflow of 100,000 (which might include all cash paid for the machinery, transportation-in and set-up expenditures, and initial employee training disbursements.) The annual net cash flow (receipts less disbursements) from this new line for years 1-12 is forecast as follows: -54672, -39161, 3054, 7128, 25927, 28838, 46088, 77076, 46726, 76852, 132332, 166047, reflecting two years of running deficits as experience and sales are built up, with net cash receipts forecast positive after that. At the end of the 12 years it's estimated that the entire line becomes obsolete and its scrap value just covers all the removal and disposal expenditures. All values are after-tax, and the required rate of return is given to be 10%. (This also makes the simplifying assumption that the net cash received or paid is lumped into a single transaction occurring on the last day of each year.)The present value (PV) can be calculated for each year:
| Year | Cash flow | Present value |
|---|---|---|
| T=0 | 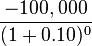 |
-100,000 |
| T=1 |  |
-49701.81818 |
| T=2 |  |
-32364.46281 |
| T=3 |  |
2294.515402 |
| T=4 |  |
4868.51991 |
| T=5 |  |
16098.62714 |
| T=6 |  |
16278.29919 |
| T=7 |  |
23650.43135 |
| T=8 |  |
35956.52284 |
| T=9 |  |
19816.38532 |
| T=10 | 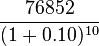 |
29629.77288 |
| T=11 |  |
46381.55871 |
| T=12 |  |
52907.69139 |
- The investment horizon of all possible projects are equally acceptable (e.g. a 3 year project is not preferable vs. a 20 year project.)
- The 10% discount rate is the appropriate rate to discount the cash flows from each project. Each project is assumed equally speculative.
- the shareholders can't get above a 10% return on their money if they were to directly assume an equivalent level of risk. (If the investor could do better elsewhere, no projects should be undertaken by the firm and the money should be given back to the shareholder through dividends and stock repurchases.)
Common pitfalls
- If, for example, the
 are generally negative late in the project (e.g.,
an industrial or mining project might have clean-up and restoration
costs), then at that stage the company owes money, so a high discount
rate is not cautious but too optimistic. Some people see this as a
problem with NPV. A way to avoid this problem is to include explicit
provision for financing any losses after the initial investment, that
is, explicitly calculate the cost of financing such losses.
are generally negative late in the project (e.g.,
an industrial or mining project might have clean-up and restoration
costs), then at that stage the company owes money, so a high discount
rate is not cautious but too optimistic. Some people see this as a
problem with NPV. A way to avoid this problem is to include explicit
provision for financing any losses after the initial investment, that
is, explicitly calculate the cost of financing such losses. - Another common pitfall is to adjust for risk by adding a premium to the discount rate. Whilst a bank might charge a higher rate of interest for a risky project, that does not mean that this is a valid approach to adjusting a net present value for risk, although it can be a reasonable approximation in some specific cases. One reason such an approach may not work well can be seen from the following: if some risk is incurred resulting in some losses, then a discount rate in the NPV will reduce the impact of such losses below their true financial cost. A rigorous approach to risk requires identifying and valuing risks explicitly, e.g., by actuarial or Monte Carlo techniques, and explicitly calculating the cost of financing any losses incurred.
- Yet another issue can result from the compounding of the risk premium. R is a composite of the risk free rate and the risk premium. As a result, future cash flows are discounted by both the risk-free rate as well as the risk premium and this effect is compounded by each subsequent cash flow. This compounding results in a much lower NPV than might be otherwise calculated. The certainty equivalent model can be used to account for the risk premium without compounding its effect on present value.
- Another issue with relying on NPV is that it does not provide an overall picture of the gain or loss of executing a certain project. To see a percentage gain relative to the investments for the project, usually, Internal rate of return or other efficiency measures are used as a complement to NPV.
- Non-specialist users frequently make the error of computing NPV based on cash flows after interest. This is wrong because it double counts the time value of money. Free cash flow should be used as the basis for NPV computations.
History
Net present value as a valuation methodology dates at least to the 19th century. Karl Marx refers to NPV as fictitious capital, and the calculation as "capitalising," writing:[6]The forming of a fictitious capital is called capitalising. Every periodically repeated income is capitalised by calculating it on the average rate of interest, as an income which would be realised by a capital at this rate of interest.In mainstream neo-classical economics, NPV was formalized and popularized by Irving Fisher, in his 1907 The Rate of Interest and became included in textbooks from the 1950s onwards, starting in finance texts.