Methods Of Determining Correlation
r = 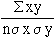
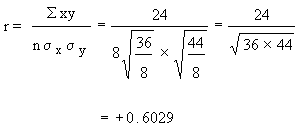
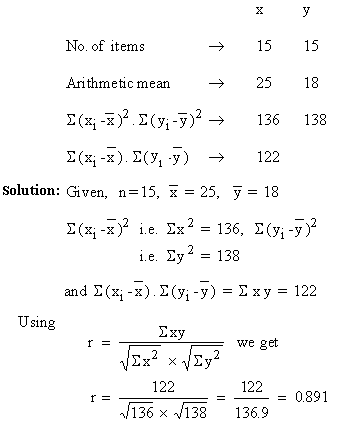
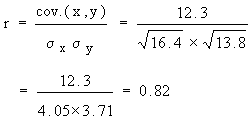
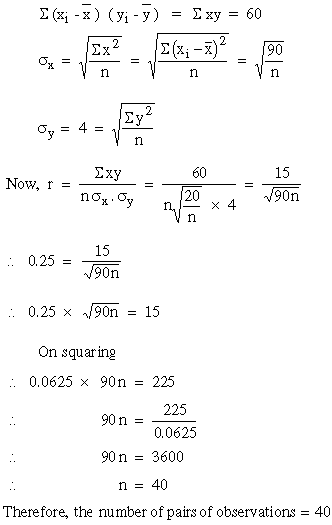
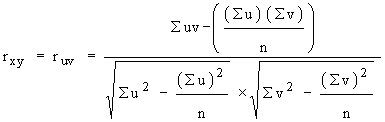
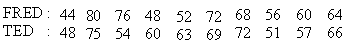 Find the coefficient of correlation between the two.
Find the coefficient of correlation between the two.
Solution: Here x0 = 60, c = 4, y0 = 60 and d = 3
We shall consider the following most commonly used methods.(1)Scatter Plot (2) Kar Pearson’s coefficient of correlation (3) Spearman’s Rank-correlation coefficient.
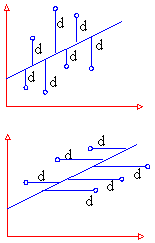
1) Scatter Plot ( Scatter diagram or dot diagram ): In this method the values of the two variables are plotted on a graph paper. One is taken along the horizontal ( (x-axis) and the other along the vertical (y-axis). By plotting the data, we get points (dots) on the graph which are generally scattered and hence the name ‘Scatter Plot’.
The manner in which these points are scattered, suggest the degree and the direction of correlation. The degree of correlation is denoted by ‘ r ’ and its direction is given by the signs positive and negative.
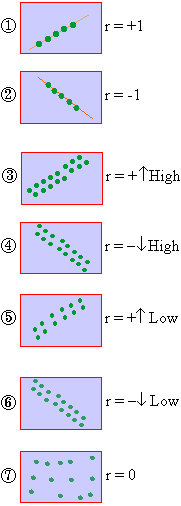 i) If all points lie on a rising straight line the correlation is perfectly positive and r = +1 (see fig.1 )
i) If all points lie on a rising straight line the correlation is perfectly positive and r = +1 (see fig.1 )
 i) If all points lie on a rising straight line the correlation is perfectly positive and r = +1 (see fig.1 )
i) If all points lie on a rising straight line the correlation is perfectly positive and r = +1 (see fig.1 )
ii) If all points lie on a falling straight line the correlation is perfectly negative and r = -1 (see fig.2)
iii) If the points lie in narrow strip, rising upwards, the correlation is high degree of positive (see fig.3)
iv) If the points lie in a narrow strip, falling downwards, the correlation is high degree of negative (see fig.4)
v) If the points are spread widely over a broad strip, rising upwards, the correlation is low degree positive (see fig.5)
vi) If the points are spread widely over a broad strip, falling downward, the correlation is low degree negative (see fig.6)
vii) If the points are spread (scattered) without any specific pattern, the correlation is absent. i.e. r = 0. (see fig.7)
Though this method is simple and is a rough idea about the existence and the degree of correlation, it is not reliable. As it is not a mathematical method, it cannot measure the degree of correlation.
2) Karl Pearson’s coefficient of correlation: It gives the numerical expression for the measure of correlation. it is noted by ‘ r ’. The value of ‘ r ’ gives the magnitude of correlation and sign denotes its direction. It is defined as
where 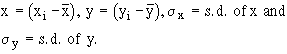
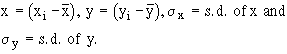
N = Number of pairs of observation
Now,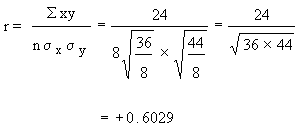
Since r is positive and 0.6. This shows that the correlation is positive and moderate (i.e. direct and reasonably good).
Example From the following data compute the coefficient of correlation between x and y.
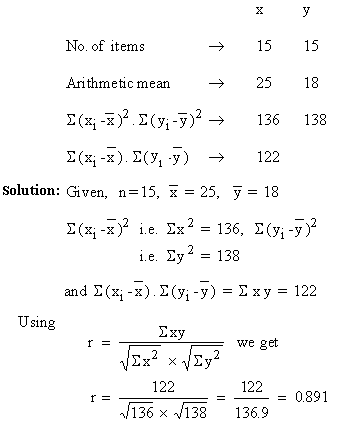
Example If covariance between x and y is 12.3 and the variance of x and y are 16.4 and 13.8 respectively. Find the coefficient of correlation between them.
Solution: Given - Covariance = cov ( x, y ) = 12.3
Variance of x ( s x2 )= 16.4
Variance of y (sy2 ) = 13.8
Now,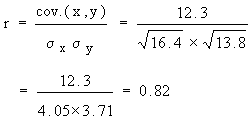
Example Find the number of pair of observations from the following data.
r = 0.25, S (xi - x ) ( yi - y ) = 60, sy = 4, S ( xi - x )2 = 90.
Solution: Given - r = 0.25
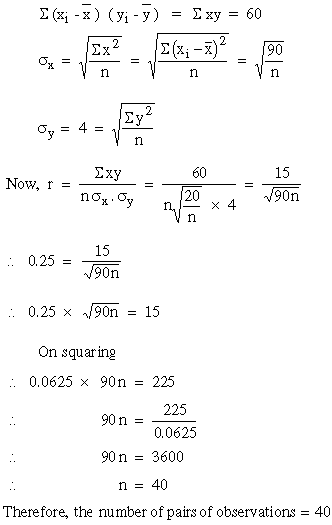
If the values of x and y are very big, the calculation becomes very tedious and if we change the variable x to u =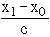 and y to
and y to 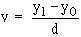 where x0 and y0 are the assumed means for variable x and y respectively, then rxy= ruv
where x0 and y0 are the assumed means for variable x and y respectively, then rxy= ruv
The formula for r can be simplified as
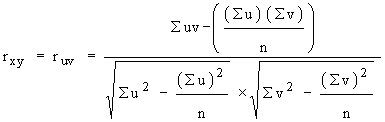
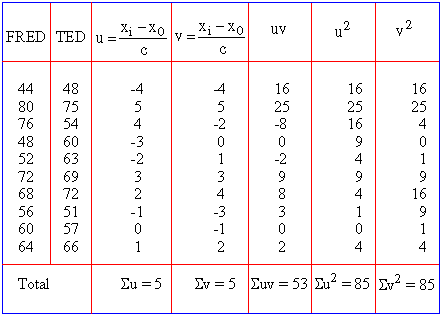
Example Marks obtained by two brothers FRED and TED in 10 tests are as follows:
Solution: Here x0 = 60, c = 4, y0 = 60 and d = 3

Calculation:
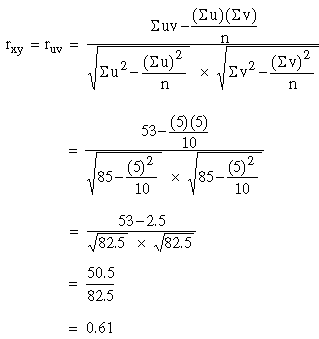
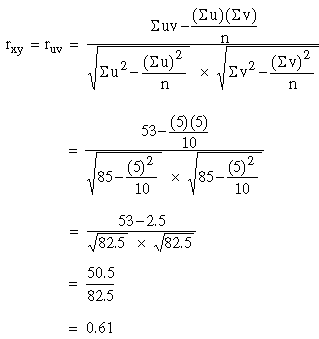
Spearman’s Rank Correlation Coefficient
This method is based on the ranks of the items rather than on their actual values. The advantage of this method over the others in that it can be used even when the actual values of items are unknown. For example if you want to know the correlation between honesty and wisdom of the boys of your class, you can use this method by giving ranks to the boys. It can also be used to find the degree of agreementsbetween the judgements of two examiners or two judges. The formula is :
R = 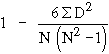
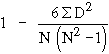
where R = Rank correlation coefficient
D = Difference between the ranks of two items
N = The number of observations.
Note: -1 £R £ 1.
i) When R = +1 Þ Perfect positive correlation or complete agreement in the same direction
ii) When R = -1 Þ Perfect negative correlation or complete agreement in the opposite direction.
iii) When R = 0 Þ No Correlation.
Computation:- Give ranks to the values of items. Generally the item with the highest value is ranked 1 and then the others are given ranks 2, 3, 4, .... according to their values in the decreasing order.
- Calculate D2 and then find S D2
- Apply the formula.
¬ Note :
In some cases, there is a tie between two or more items. in such a case each items have ranks 4th and 5th respectively then they are given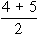 = 4.5th rank. If three items are of equal rank say 4th then they are given
= 4.5th rank. If three items are of equal rank say 4th then they are given 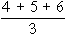 = 5th rank each. If m be the number of items of equal ranks, the factor
= 5th rank each. If m be the number of items of equal ranks, the factor 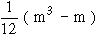 is added to S D2. If there are more than one of such cases then this factor added as many times as the number of such cases, then
is added to S D2. If there are more than one of such cases then this factor added as many times as the number of such cases, then
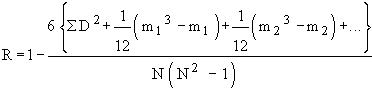
Example Calculate ‘ R ’ from the following data.
StudentNo.: 12345678910Rank in Maths : 13754621098Rank in Stats:
Solution :
Example Calculate ‘ R ’ of 6 students from the following data.
Solution:
Here m = 2 since in series of marks in English of items of values 43 repeated twice.
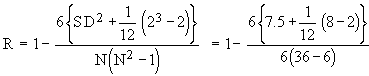
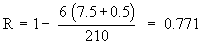
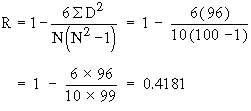
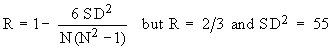
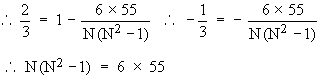
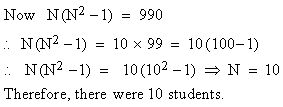 Linear Regression
Linear Regression
Student
No. |
Rank in
Maths (R1) |
Rank in
Stats (R2) |
R1 - R2D
|
(R1 - R2 )2D2
|
1
|
1
|
3
|
-2
|
4
|
2
|
3
|
1
|
2
|
4
|
3
|
7
|
4
|
3
|
9
|
4
|
5
|
5
|
0
|
0
|
5
|
4
|
6
|
-2
|
4
|
6
|
6
|
9
|
-3
|
9
|
7
|
2
|
7
|
-5
|
25
|
8
|
10
|
8
|
2
|
4
|
9
|
9
|
10
|
-1
|
1
|
10
|
8
|
2
|
6
|
36
|
N = 10
|
S D = 0
|
S D2 = 96
|
Calculation of R :
Marks in Stats :
|
40
|
42
|
45
|
35
|
36
|
39
|
Marks in English :
|
46
|
43
|
44
|
39
|
40
|
43
|
Marks in Stats
|
R1
|
Marks in English
|
R2
|
R1 - R2
|
(R1 -R2)2=D2
|
40
|
3
|
46
|
1
|
2
|
4
|
42
|
2
|
43
|
3.5
|
-1.5
|
2.25
|
45
|
1
|
44
|
2
|
-1
|
1
|
35
|
6
|
39
|
6
|
0
|
0
|
36
|
5
|
40
|
5
|
0
|
0
|
39
|
4
|
43
|
3.5
|
0.5
|
0.25
|
N = 6
|
S D = 0
|
S D2 = 7.50
|
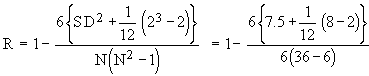
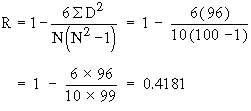
Example The value of Spearman’s rank correlation coefficient for a certain number of pairs of observations was found to be 2/3. Thesum of the squares of difference between the corresponding rnks was 55. Find the number of pairs.
Solution: We have
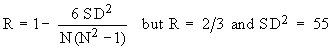
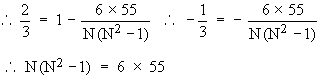
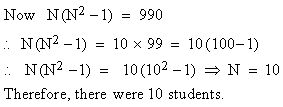
Correlation gives us the idea of the measure of magnitude and direction between correlated variables. Now it is natural to think of a method that helps us in estimating the value of one variable when the other is known. Also correlation does not imply causation. The fact that the variables x and y are correlated does not necessarily mean that x causes y or vice versa. For example, you would find that the number of schools in a town is correlated to the number of accidents in the town. The reason for these accidents is not the school attendance; but these two increases what is known as population. A statistical procedure called regression is concerned with causation in a relationship among variables. It assesses the contribution of one or more variable calledcausing variable or independent variable or one which is beingcaused (dependent variable). When there is only one independent variable then the relationship is expressed by a straight line. This procedure is called simple linear regression.
Regression can be defined as a method that estimates the value of one variable when that of other variable is known, provided the variables are correlated. The dictionary meaning of regression is "to go backward." It was used for the first time by Sir Francis Galton in hisresearch paper "Regression towards mediocrity in hereditary stature."
Lines of Regression: In scatter plot, we have seen that if the variables are highly correlated then the points (dots) lie in a narrow strip. if the strip is nearly straight, we can draw a straight line, such that all points are close to it from both sides. such a line can be taken as an ideal representation of variation. This line is called the line of best fit if it minimizes the distances of all data points from it.
This line is called the line of regression. Now prediction is easy because now all we need to do is to extend the line and read the value. Thus to obtain a line of regression, we need to have a line of best fit. But statisticians don’t measure the distances by dropping perpendiculars from points on to the line. They measure deviations ( or errors or residuals as they are called) (i) vertically and (ii) horizontally. Thus we get two lines of regressions as shown in the figure (1) and (2).

(1) Line of regression of y on x
Its form is y = a + b x
It is used to estimate y when x is given
(2) Line of regression of x on y
Its form is x = a + b y
It is used to estimate x when y is given.
They are obtained by (1) graphically - by Scatter plot (ii) Mathematically - by the method of least squares.


